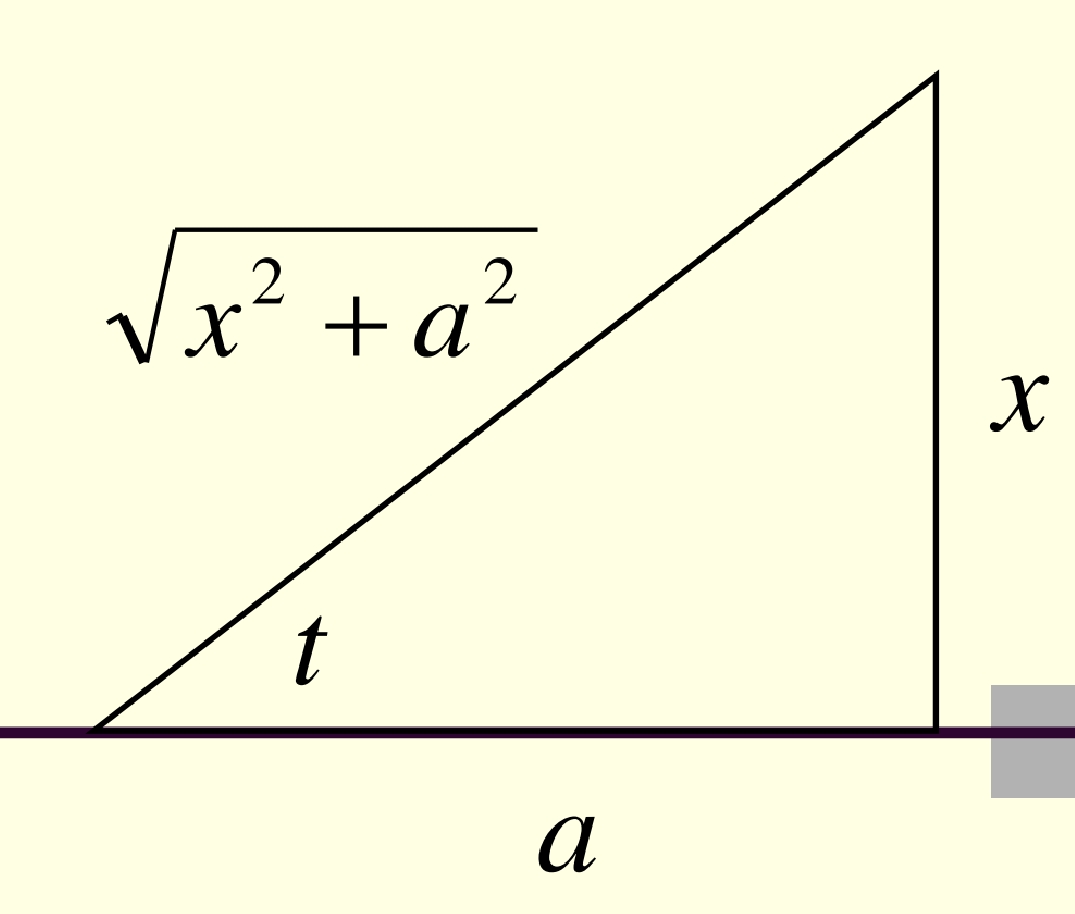MA.4.1 不定积分及其基本计算方法

一、基本概念

graph LR
原函数[原函数]-- 求导 --> 被积函数
被积函数 -- 不定积分 --> 原函数

原函数

全体原函数

Proof:

$(F(x)+c{)}^{\prime }=F^{\prime }(x):=f(x)$

令$G(x)$ 为$f(x)$任意原函数

$\therefore G^{\prime }(x)=f(x)=F^{\prime }(x)(x\in I)$

$\stackrel{\mathrm{\exists }C\in \mathbb{R}}{\Rightarrow }G(x)=F(x)+C$

不定积分

• ${\displaystyle \int }$ 一不定积分号
• $f(x)$ 一被积函数
• $x$ 一积分变量

被积表达式

不定积分与微分运算互逆

Proof:

$(\ast )$ 若$f$可导, 则 $$\displaystyle \int f^{\prime}(x) d x=f(x)+C$$

即: $$\displaystyle \int d(f(x)+C)=f(x)+C$$

若 $f$ 存在原函数, 则 $$\left(\int f(x) d x\right)^{\prime}=f(x)$$

即: $$d \int f(x) d x=f(x) d x$$

不定积分的线性运算

不定积分表

1. ${\displaystyle \int k\mathrm{d}x=kx+C(\int 0\mathrm{d}x=C)}$;

2. ${\displaystyle \int x^{\alpha }\mathrm{d}x=\frac{1}{\alpha +1}{x}^{\alpha +1}+C(\alpha \ne -1)}$;
   常用形式：

   • ${\displaystyle \int x\mathrm{d}x=\frac{1}{2}{x}^2}$

   • ${\displaystyle \int \sqrt{x}\mathrm{d}x=\frac{2}{3}{x}^{\frac{3}{2}}+C}$

   • ${\displaystyle \int \frac{\mathrm{d}x}{\sqrt{x}}=2x^{\frac{1}{2}}+C=2\sqrt{x}+C}$

   • ${\displaystyle \int \frac{\mathrm{d}x}{x^2}=-x^{-1}+C=-\frac{1}{x}+C}$

3. ${\displaystyle \int \frac{1}{x}\mathrm{d}x=\ln |x|+C}$;

   • ${\displaystyle \int \frac{1}{ax+b}\mathrm{d}x=\frac{\ln (ax+b)}{a}}$

4. ${\displaystyle \int a^x\mathrm{d}x=\frac{a^x}{\ln a}+C(0<a\ne 1)}$;

5. ${\displaystyle \int {\mathrm{e}}^x\mathrm{d}x={\mathrm{e}}^x+C}$;

6. ${\displaystyle \int \sin x\mathrm{d}x=-\cos x+C}$;

7. ${\displaystyle \int \cos x\mathrm{d}x=\sin x+C}$;

8. ${\displaystyle \int {\sec }^{2}x\mathrm{d}x=\tan x+C}$;

   • ${\displaystyle \int \sec x\mathrm{d}x=\ln |\sec x+\tan x|}$

9. ${\displaystyle \int {\csc }^{2}x\mathrm{d}x=-\cot x+C}$;

   • ${\displaystyle \int \csc x\mathrm{d}x=\ln (\tan \frac{x}{2})}$

10. ${\displaystyle \int \frac{\mathrm{d}x}{a^2+x^2}=\frac{1}{a}\arctan \frac{x}{a}+C(a\ne 0)}$;

    P.S. ${(\frac{1}{a}\arctan \frac{x}{a})}^{\prime }=\frac{1}{a}\cdot \frac{1}{a}\frac{1}{1+{\left(\frac{x}{a}\right)}^2}=\frac{1}{a^2+x^2}$

    • ${\displaystyle \int \frac{\mathrm{d}x}{1+x^2}=\arctan x+C}$

11. ${\displaystyle \int \frac{\mathrm{d}x}{x^2-a^2}=\frac{1}{2a}\ln \left|\frac{x-a}{x+a}\right|+C(a\ne 0)}$;

    • ${\displaystyle \int \frac{dx}{a^2-x^2}=\frac{1}{2a}\ln \left|\frac{x+a}{x-a}\right|+C}$

12. ${\displaystyle \int \frac{\mathrm{d}x}{\sqrt{a^2-x^2}}=\arcsin \frac{x}{a}+C(a>0)}$;

13. ${\displaystyle \int \frac{\mathrm{d}x}{\sqrt{x^2\pm a^2}}=\ln |x+\sqrt{x^2\pm a^2}|+C}$.

补充不定积分

• $\int \tan (x)\mathrm{d}x=\ln (\cos (x))$

例题

Solution

$$\begin{array}{rl}=& \int \frac{dx}{\sqrt{x}}-\int \frac{dx}{\sqrt{1-x^2}}\\ =& 2\sqrt{x}-\arcsin x+c& \end{array}$$

Solution

$$\begin{array}{rl}& =\int \frac{{\sin }^{2}x+{\cos }^{2}x}{{\sin }^{2}x{\cos }^{2}x}dx\\ & =\int (\frac{1}{{\sin }^{2}x}+\frac{1}{{\cos }^{2}x})dx\\ & =\int ({\csc }^{2}x+{\sec }^{2}x)dx\\ & =-\cot x+\tan x+C& \end{array}$$

Solution

$$\begin{array}{rl}& =\int (\frac{1}{x^2}-\frac{1}{1+x^2})dx\\ & =-\frac{1}{x}-\arctan x+C& \end{array}$$

二、换元积分法

第一代换法 / 凑微分法

• 分析

  Analysis

  $$\begin{array}{rl}& [F(\phi (x)){]}^{\prime }=f(\phi (x)){\phi }^{\prime }(x)\\ \Rightarrow & \int f(\phi (x)){\phi }^{\prime }(x)dx=F(\phi (x))+C& \end{array}$$

• 运算步骤$$$$\int f(\varphi(x)) \textcolor{orange}{\varphi^{\prime}(x) \mathrm{d} x}&=\int f(\varphi(x)) \textcolor{orange}{\mathrm{d} \varphi(x)} \
  &\xlongequal{u=\textcolor{orange}{\varphi(x)}}\int f(\textcolor{orange}u) \mathrm{d} \textcolor{orange}u=F(u)+C \
  &\xlongequal{\text{回代}}F(\textcolor{orange}{\varphi(x)})+C .
  \end$$$$

Solution

$$\begin{array}{rl}& =\int \frac{\sin x}{\cos x}dx\\ & =\int \frac{-d\cos x}{\cos x}\\ & \stackrel{u=-\cos x}{=}-\int \frac{du}{u}\\ & =-\ln |u|+C\\ & =-\ln |\cos x|+C& \end{array}$$

Solution

$$\begin{array}{rl}& =\int {(2x-1)}^{20}\cdot \frac{1}{2}d(2x-1)\\ & \stackrel{u=2x-1}{=}\frac{1}{2}{u}^{10}du\\ & =\frac{u^{11}}{22}+C\\ & =\frac{(2x-1{)}^{11}}{22}+C& \end{array}$$

Solution

$$\begin{array}{rl}=& \frac{1}{a}\int \frac{\frac{1}{a}dx}{1+{\left(\frac{x}{a}\right)}^2}\\ =& \frac{1}{a}\int \frac{d\frac{x}{a}}{1+{\left(\frac{x}{a}\right)}^2}\\ =& \frac{1}{a}\int \frac{du}{1+u^2}\\ =& \frac{1}{a}\arctan \frac{x}{a}+C& \end{array}$$

Solution

$$\begin{array}{rl}=& \int \frac{dx}{(x-a)(x+a)}\\ =& \frac{1}{2a}\int (\frac{1}{x-a}-\frac{1}{x+a})dx\\ =& \frac{1}{2a}(\int \frac{d(x-a)}{x-a}-\int \frac{d(x+a)}{x+a})\\ =& \frac{1}{2a}[\ln |x-a|-\ln |x+a|]\\ =& \frac{1}{2a}\ln \left|\frac{x-a}{x+a}\right|+C& \end{array}$$

Solution 凑微分

$$\begin{array}{rl}=& \int \frac{1}{\cos x}dx\\ =& \int \frac{\cos x}{{\cos }^{2}x}dx\to \text{ 凑 }\sin x\\ =& \int \frac{d\sin x}{1-{\sin }^{2}x}\to \int \frac{\mathrm{d}x}{a^2-x^2}=\frac{1}{2a}\ln \left|\frac{x+a}{x-a}\right|+C(a\ne 0)\\ =& \frac{1}{2}\ln \left|\frac{1+\sin x}{1-\sin x}\right|+C\\ =& \frac{1}{2}\ln \frac{(1+\sin x{)}^2}{{\cos }^{2}x}+C\\ =& \ln \left|\frac{1+\sin x}{\cos x}\right|+C\\ =& \ln |\sec x+\tan x|+C& \end{array}$$

Solution 添项

$$\begin{array}{r}\\ & \int {\displaystyle \frac{\ln x}{x\sqrt{1+\ln x}}}dx\\ & =\int {\displaystyle \frac{\ln x\cdot d\ln x}{\sqrt{1+\ln x}}}\\ & \stackrel{u=\ln x}{=}\int \frac{(1+u-1)du}{\sqrt{1+u}}\\ & =\int (\sqrt{1+u}-\frac{1}{\sqrt{1+u}})d(1+u)\\ & =\frac{2}{3}(1+u{)}^{3/2}-2\sqrt{1+u}+C\\ & =\frac{2}{3}(1+\ln x{)}^{3/2}-2\sqrt{1+\ln x}+C& \end{array}$$

Solution 配方

$$\begin{array}{rl}=& \int \frac{2x-4+3}{x^2-4x+5}dx\\ =& \int \frac{d(x^2-4x+5)}{x^2-4x+5}+\int \frac{3}{(x-2{)}^2+1}d(x-2)\\ =& \ln |x^2-4x+5|+3\arctan (x-2)+C& \end{array}$$

Solution

分式上下同时除去$x^2$，凑微分+配方：

$$\begin{array}{rl}& =\int \frac{(1+\frac{1}{x^2})dx}{x^2+1+\frac{1}{x^2}}\\ & =\int \frac{d(x-\frac{1}{x})}{{(x-\frac{1}{x})}^2+{\sqrt{3}}^2}\\ & =\frac{1}{\sqrt{3}}\arctan \frac{x-\frac{1}{x}}{\sqrt{3}}+C& \end{array}$$

注意到，该式在$x=0$时无意义，继续补充

设 $f(x)={\displaystyle \frac{x^2+1}{x^4+x^2+1}}$ 原函数为 $F(x)$

$$\therefore F(x)=\{\begin{array}{ll}\frac{1}{\sqrt{3}}\arctan \frac{x-\frac{1}{x}}{\sqrt{3}}+C_1,& x>0\\ \\ C,& x=0\\ \\ \frac{1}{\sqrt{3}}\arctan \frac{x-\frac{1}{x}}{\sqrt{3}}+C_2,& x<0\end{array}$$$$\begin{array}{rl}& \because F(x)\text{ 在 }x=0\text{ 连续. }\\ & \therefore F(0+0)=F(0)=F(0-0),\text{此时}x-\frac{1}{x}\text{趋近正负无穷}\\ & \Rightarrow \frac{1}{\sqrt{3}}\cdot (-\frac{\pi }{2})+C_1=C=\frac{1}{\sqrt{3}}\cdot \frac{\pi }{2}+C_2\\ & \therefore C_1=C+\frac{1}{\sqrt{3}}\cdot \frac{\pi }{2}\\ & C_2=C-\frac{1}{\sqrt{3}}\cdot \frac{\pi }{2}& \end{array}$$

从而原函数 $F(x)=\{\begin{array}{ll}{\displaystyle \frac{1}{\sqrt{3}}}\arctan {\displaystyle \frac{x-\frac{1}{x}}{\sqrt{3}}}+{\displaystyle \frac{1}{\sqrt{3}}}\cdot {\displaystyle \frac{\pi }{2}}+C,& x\ge 0\\ {\displaystyle \frac{1}{\sqrt{3}}}\arctan {\displaystyle \frac{x-\frac{1}{x}}{\sqrt{3}}}-{\displaystyle \frac{1}{\sqrt{3}}}\cdot {\displaystyle \frac{\pi }{2}}+C,& x<0\end{array}$

下说明 $F^{\prime }(x){|}_{x=0}=f(0)$
由于 $\underset{x\to 0}{lim}{F}^{\prime }(x)=\underset{x\to 0}{lim}f(x)=f(0)=1$
又$\because F(x)$ 在 $x=0$ 连续：
$\Rightarrow F^{\prime }(0)=f(0)=1$ （运用 #导数极限定理: 导函数极限->导数极限）

第二代换法/换元积分法

已知右端求左端积分为第一代换法; 已知左端, 能否求右端积分呢? 此即下面的第二换元法.

• 运算步骤

• 证明

Proof

$$\begin{array}{rl}& \frac{d}{dx}G({\phi }^{-1}(x))\\ & \stackrel{t:={\phi }^{-1}(x)}{=}{G}^{\prime }(t)\frac{dt}{dx}\\ & =G^{\prime }(t)\cdot \frac{1}{\frac{dx}{dt}}\\ & =f(\phi (t)){\phi }^{\prime }(t)\cdot \frac{1}{{\phi }^{\prime }(t)}=f(\phi (t))\\ & =f(x)& \end{array}$$

例题

#三角代换 去根号

Solution

$\text{令 }x=a\tan t,|t|<\frac{\pi }{2}$

$$\begin{array}{rl}\int \frac{\mathrm{d}x}{\sqrt{x^2+a^2}}& =\int \frac{a{\sec }^{2}t\mathrm{d}t}{\sqrt{a^2{\tan }^{2}t+a^2}}\\ & =\int \frac{{\sec }^{2}t}{\sqrt{{\sec }^{2}t}}dt\\ & =\int \sec tdt\\ & =\ln |\sec t+\tan t|+C\\ & =\ln |\frac{\sqrt{x^2+a^2}}{a}+\frac{x}{a}|+C\\ & =\ln |x+\sqrt{x^2+a^2}|+C_1& \end{array}$$

Tip

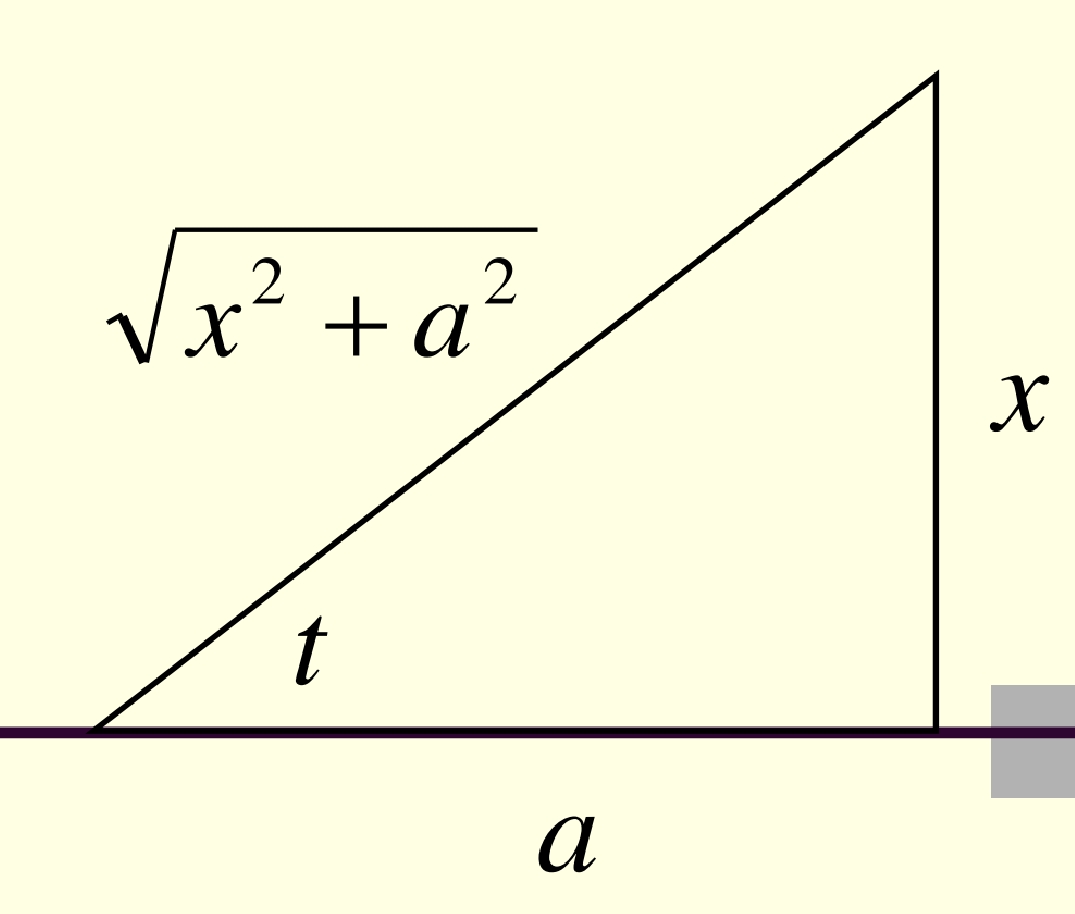
Solution

$$\begin{array}{rl}\mathrm{令}x& =a\sin t\\ \mathrm{原}\mathrm{式}& =\int \sqrt{a^2-a^2{\sin }^{2}t}(a\cos tdt)\\ & =a^2\int {\cos }^{2}tdt\\ & =\frac{a^2}{2}\int (1+{\cos }^{2}t)dt\\ & =\frac{a^2}{2}(t+\frac{\sin 2t}{2})+c\\ & =\frac{a^2}{2}t+\frac{a^2}{2}\sin t\cos t+c\\ & =\frac{a^2}{2}\arcsin \frac{x}{a}+\frac{a^2}{2}\cdot \frac{x}{a}\cdot \sqrt{1-\frac{x^2}{a^2}}+C\\ & =\frac{a^2}{2}\arcsin \frac{x}{a}+\frac{x}{2}\sqrt{a^2-x^2}+c& \end{array}$$

Solution

法I.配方

$$\begin{array}{rl}\mathrm{原}\mathrm{式}& =\int \frac{d(x-\frac{1}{2})}{\sqrt{{\left(\frac{1}{2}\right)}^2-{(x-\frac{1}{2})}^2}}\\ & =\arcsin (2x-1)& \end{array}$$

或:

法II.灵机一动
注意到： ${\sin }^{2}x+{\cos }^x=x+(1-x)=1$
$\mathrm{令}x={\sin }^{2}t,t\in (0,\frac{\pi }{2})$

$$\begin{array}{rl}\therefore \text{ 原式 }& =\int \frac{2\sin t\cos t\mathrm{d}t}{\sqrt{{\sin }^{2}t{\cos }^{2}t}}\\ & =2\int \mathrm{d}t\\ & =2t+C\\ & =2\arcsin \sqrt{x}+C& \end{array}$$

Tip
上述例子很好地说明了原函数可不唯一（$C$不同）

#倒数代换

Solution

$$\begin{array}{rl}& \underset{t>0}{\overset{x=1/t}{=}}\int \frac{-\frac{1}{t^2}dt}{\frac{1}{t}\sqrt{\frac{1}{t^2}+\frac{1}{t}+1}}\\ & =-\int \frac{dt}{\sqrt{1+t+t^2}}\\ & =-\int \frac{d(t+\frac{1}{2})}{\sqrt{{(t+\frac{1}{2})}^2+\frac{3}{4}}}\\ & =-\ln |t+\frac{1}{2}+\sqrt{1+t+t^2}|+C\\ & =-\ln |\frac{1}{x}+\frac{1}{2}+\frac{\sqrt{x^2+x+1}}{x}|+C& \end{array}$$

三、分部积分法

• 记忆
  • ${\displaystyle \int u(x)\mathrm{d}v(x)=u(x)v(x)-\int v(x)\mathrm{d}u(x)}$.
  • 前后相乘 - ∫ 交换位置
• 凑微分函数依次是: 指数函数, 三角函数, 幕函数,对数函数, 反三角函数.
• 证明

Proof

$$\begin{array}{rl}& (u(x)v(x){)}^{\prime }=u^{\prime }(x)v(x)+u(x)v^{\prime }(x)\\ & \text{ 有 }\int [u^{\prime }(x)v(x)+u(x)v^{\prime }(x)]=u(x)v(x)+c\\ & \text{ 即: }\int u(x)dv(x)=u(x)v(x)-\int v(x)du(x)& \end{array}$$

例题

Solution

$$\begin{array}{rl}& =x\ln x-\int xd\ln x\\ & =x\ln x-\int x\cdot \frac{1}{x}dx\\ & =x\ln x-x+C& \end{array}$$

Solution

$$\begin{array}{rlr}I& =\int {\mathrm{e}}^x\sin x\mathrm{d}x& e^x,\mathrm{d}x\mathrm{合}\mathrm{并}\\ & =\int \sin x\mathrm{d}{e}^x& \mathrm{分}\mathrm{部}\mathrm{积}\mathrm{分}\\ & =e^x\sin x-\int e^x\mathrm{d}\sin x& e^x,\mathrm{d}x\mathrm{合}\mathrm{并}\\ & =e^x\sin x-\int \cos x\mathrm{d}{e}^x& \mathrm{分}\mathrm{部}\mathrm{积}\mathrm{分}\\ & =e^x\sin x-e^x\cos x+\int e^x\mathrm{d}\cos x\\ & =e^x(\sin x-\cos x)-\underbrace{\int \sin x\mathrm{d}{e}^x}\\ \therefore I& =e^x(\sin x-\cos x)-I\\ \therefore 2I& =e^x(\sin x-\cos x)+C\\ I& =\frac{1}{2}{e}^x(\sin x-\cos x)+C& \end{array}$$

Solution

$$\begin{array}{rl}{I}_n& =\frac{\alpha }{{(x^2+a^2)}^n}-(-2\int \frac{(x^2+a^2-a^2}{{(x^2+a^2)}^{n+1}}dx)\\ & =\frac{x}{(x^2+a^2)}+2n{I}_n-2n{a}^2{I}_{n+1}\\ \Rightarrow I_n& =\frac{x}{2n{a}^2{(x^2+a^2)}^n}+\frac{2n-1}{2n{a}^2}{I}_n& \end{array}$$

其中: $I_1=\frac{1}{a}\arctan \frac{x}{a}$

Solution

$$\begin{array}{rl}& I=\int x{(1+e^x)}^{-\frac{3}{2}}d(e^x+1)\\ & =-2\int xd{(1+e^x)}^{-\frac{1}{2}}\\ & =-\frac{2x}{\sqrt{1+e^x}}+2\int \frac{1}{\sqrt{1+e^x}}dx\\ & \text{ 其中 }\int \frac{1}{\sqrt{1+e^x}}dx\end{array}$$

故原式 $=-\frac{2x}{\sqrt{1+e^x}}+2\int \frac{1}{\sqrt{1+e^2}}dx$

$=-\frac{2x}{\sqrt{1+e^{-2}}}+\ln \left|\frac{\sqrt{10x-1}-1}{\sqrt{1+c^2+1}}\right|+c$

Soution

$$\begin{array}{l}\begin{array}{c}\text{Take the integral:}\\ \int \frac{x}{{(x^2+1)}^{3/2}}dx\end{array}\\ \begin{array}{c}\text{For }\text{the }\text{integrand }\frac{x}{{(x^2+1)}^{3/2}},\text{substitute }u=x^2+1\text{ and }du=2xdx:\\ \text{= }\frac{1}{2}\int \frac{1}{u^{3/2}}du\end{array}\\ \begin{array}{c}\text{The }\text{integral }\text{of }\frac{1}{u^{3/2}}\text{is }-\frac{2}{\sqrt{u}}:\\ \text{= }-\frac{1}{\sqrt{u}}+\text{constant}\end{array}\\ \begin{array}{c}\text{Substitute }\text{back }\text{for }u=x^2+1:\\ \boxed{\begin{array}{ll}\text{Answer:}& \\ & \text{= }-\frac{1}{\sqrt{x^2+1}}+\text{constant}\end{array}}\end{array}\end{array}$$

Solution

$$\begin{array}{l}\begin{array}{c}\text{For }\text{the }\text{integrand }\frac{x\log (x)}{{(x^2+1)}^{3/2}},\text{integrate }\text{by }\text{parts, }\int fdg=fg-\int gdf,\text{where }\\ f=\log (x),dg=\frac{x}{{(x^2+1)}^{3}2}dx,df=\frac{1}{x}dx,\\ g=\frac{1}{\sqrt{x^2+1}}:\\ \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}+\int \frac{1}{x\sqrt{x^2+1}}dx\end{array}\\ \\ \begin{array}{c}\text{For }\text{the }\text{integrand }\frac{1}{x\sqrt{x^2+1}},\text{substitute }x=\tan (u)\text{and }dx={\sec }^2(u)du.\\ \text{Then }\sqrt{x^2+1}\text{= }\sqrt{{\tan }^2(u)+1}\text{= }\sec (u)\text{and }u={\tan }^{-1}(x):\\ \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}+\int \csc (u)du\end{array}\\ \\ \begin{array}{c}\text{Multiply }\text{numerator }\text{and }\text{denominator }\text{of }\csc (u)\text{by }\cot (u)+\csc (u):\\ \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}+\int -\frac{-\cot (u)\csc (u)-{\csc }^2(u)}{\cot (u)+\csc (u)}du\end{array}\\ \\ \begin{array}{c}\text{For }\text{the }\text{integrand }-\frac{-\cot (u)\csc (u)-{\csc }^2(u)}{\cot (u)+\csc (u)},\text{substitute }s=\cot (u)+\csc (u)\text{and }\\ ds=(-{\csc }^2(u)-\cot (u)\csc (u))du:\\ \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}+\int -\frac{1}{s}ds\end{array}\\ \\ \begin{array}{c}\text{Factor }\text{out }\text{constants:}\\ \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}-\int \frac{1}{s}ds\end{array}\\ \\ \begin{array}{c}\text{The }\text{integral }\text{of }\frac{1}{s}\text{is }\log (s):\\ \text{= }-\log (s)-\frac{\log (x)}{\sqrt{x^2+1}}+\text{constant}\end{array}\\ \\ \begin{array}{c}\text{Substitute }\text{back }\text{for }s=\cot (u)+\csc (u):\\ \text{= }-\log (\cot (u)+\csc (u))-\frac{\log (x)}{\sqrt{x^2+1}}+\text{constant}\end{array}\\ \\ \begin{array}{c}\text{Substitute }\text{back }\text{for }u={\tan }^{-1}(x):\\ \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}-\log (\cot ({\tan }^{-1}(x))+\csc ({\tan }^{-1}(x)))+\text{constant}\end{array}\\ \\ \begin{array}{c}\text{Simplify }\text{using }\cot ({\tan }^{-1}(z))=\frac{1}{z}\text{and }\csc ({\tan }^{-1}(z))=\frac{\sqrt{z^2+1}}{z}:\\ \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}-\log \left(\frac{\sqrt{x^2+1}+1}{x}\right)+\text{constant}\end{array}\\ \\ \begin{array}{c}\text{An }\text{alternative }\text{form }\text{of }\text{the }\text{integral }\text{is:}\\ \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}-{\text{csch}}^{-1}(x)+\text{constant}\end{array}\\ \\ \begin{array}{c}\text{Which }\text{is }\text{equivalent }\text{for }\text{restricted }x\text{values }\text{to:}\\ \boxed{\begin{array}{ll}\text{Answer:}& \\ & \text{= }-\frac{\log (x)}{\sqrt{x^2+1}}-\log (\sqrt{x^2+1}+1)+\log (x)+\text{constant}\end{array}}\end{array}\end{array}$$

TIP
实际上可以使用 #三角代换 $x=\tan t$ 配合 #万能变换 $u=\tan (t/2)$
简略过程如下：
$\mathrm{令}x=\tan t,|t|<\frac{\pi }{2}$

$$\begin{array}{rl}\text{原式}& =\cdots +\int \frac{1}{\sqrt{{\tan }^{2t+1}}\tan t}\mathrm{d}t\\ & =\int \csc t\mathrm{d}t\end{array}$$